المحتوى
- أساسيات الدوائر الكهربائية
- سلسلة مقابل الدوائر الموازية
- حساب المقاومة لدائرة السلسلة
- حساب المقاومة لدائرة موازية
- كيفية حل سلسلة ودائرة الجمع الموازي
- حسابات أخرى
إن التعرف على أساسيات الإلكترونيات يعني فهم الدوائر وكيفية عملها وكيفية حساب أشياء مثل المقاومة الكلية حول أنواع مختلفة من الدوائر. يمكن أن تصبح الدوائر في العالم الحقيقي معقدة ، ولكن يمكنك فهمها بالمعرفة الأساسية التي تلتقطها من دوائر أبسط مثالية.
النوعان الرئيسيان من الدوائر هما سلسلة ومتوازية. في دائرة متسلسلة ، يتم ترتيب جميع المكونات (مثل المقاومات) في خط ، مع حلقة واحدة من الأسلاك التي تشكل الدائرة. تنقسم الدائرة المتوازية إلى مسارات متعددة مع مكون واحد أو أكثر على كل منها. يعد حساب دوائر السلسلة أمرًا سهلاً ، لكن من المهم فهم الاختلافات وكيفية التعامل مع كلا النوعين.
أساسيات الدوائر الكهربائية
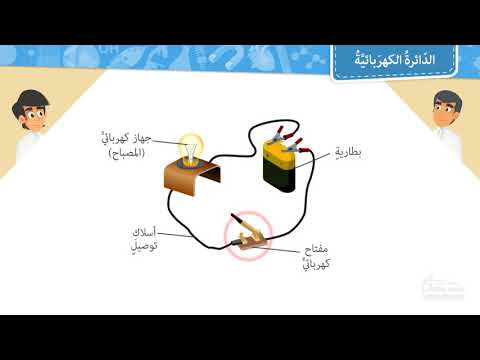
الكهرباء تتدفق فقط في الدوائر. بمعنى آخر ، يحتاج إلى حلقة كاملة لكي يعمل شيء ما. إذا قطعت هذه الحلقة بمفتاح ، فإن الطاقة تتوقف عن التدفق ، وسوف ينطفئ الضوء (على سبيل المثال). تعريف الدائرة البسيطة هو حلقة مغلقة لموصل يمكن للإلكترونات التنقل حولها ، تتكون عادةً من مصدر طاقة (بطارية ، على سبيل المثال) ومكون كهربائي أو جهاز (مثل المقاوم أو المصباح الكهربائي) وسلك موصل.
ستحتاج إلى التعرف على بعض المصطلحات الأساسية لفهم كيفية عمل الدوائر ، لكنك ستكون على دراية بمعظم المصطلحات من الحياة اليومية.
"فرق الجهد" هو مصطلح للاختلاف في الطاقة الكهربائية المحتملة بين مكانين لكل وحدة شحن. تعمل البطاريات عن طريق إحداث فرق في الإمكانات بين مطاريها ، مما يسمح للتيار بالتدفق من واحد إلى الآخر عندما يكون متصلاً في دائرة. الجهد في نقطة ما هو الجهد من الناحية الفنية ، ولكن الاختلافات في الجهد هي الشيء المهم في الممارسة. تحتوي البطارية ذات 5 فولت على اختلاف محتمل قدره 5 فولت بين المحطتين ، و 1 فولت = جول لكل كولوم.
يؤدي توصيل موصل (مثل السلك) بكلا طرفي البطارية إلى إنشاء دائرة ، مع تدفق التيار الكهربائي حولها. يقاس التيار بالأمبير ، مما يعني كولوم (الشحن) في الثانية.
سيكون لأي موصل "مقاومة" كهربائية ، مما يعني معارضة المادة لتدفق التيار. تقاس المقاومة بالأوم (Ω) ، والموصل ذو المقاومة 1 أوم المتصل عبر فولطية قدرها 1 فولت سوف يسمح بتدفق تيار يبلغ 1 أمبير.
العلاقة بين هذين النوعين مغلفة بقانون أوم:
الخامس = IR
بمعنى ، "الجهد يساوي التيار مضروبًا بالمقاومة".
سلسلة مقابل الدوائر الموازية
يتميز النوعان الرئيسيان للدوائر بكيفية ترتيب المكونات فيها.
تعريف دائرة سلسلة بسيط هو "دائرة مع المكونات مرتبة في خط مستقيم ، وبالتالي فإن كل التيار يتدفق من خلال كل مكون بدوره." إذا قمت بإجراء دائرة حلقة أساسية مع بطارية متصلة اثنين من المقاومات ، وبعد ذلك اتصال يعمل مرة أخرى إلى البطارية ، فإن اثنين من المقاومات تكون في سلسلة. لذا ، ينتقل التيار من الطرف الموجب للبطارية (من خلال المصطلح الذي تعامله بالتيار كما لو كان من النهاية الموجبة) إلى المقاوم الأول ، ومن ذلك إلى المقاوم الثاني ثم يعود إلى البطارية.
دائرة موازية مختلفة. دائرة مع اثنين من المقاومة على التوازي ستقسم إلى مسارين ، مع المقاوم على كل منهما. عندما يصل التيار إلى مفترق طرق ، فإن نفس مقدار التيار الذي يدخل التقاطع يجب أن يترك الوصلة أيضًا. وهذا ما يسمى الحفاظ على تهمة ، أو خصيصا للإلكترونيات ، قانون كيرشوف الحالي. إذا كان المساران لهما مقاومة متساوية ، فسوف يتدفق تيار مساوٍ لأسفل ، لذا إذا وصل 6 أمبير من التيار إلى مفرق بمقاومة متساوية على كلا المسارين ، فإن 3 أمبير سوف يتدفق لأسفل لكل منهما. ثم تنضم المسارات قبل إعادة الاتصال بالبطارية لإكمال الدائرة.
حساب المقاومة لدائرة السلسلة
حساب المقاومة الكلية من مقاومات متعددة يؤكد على التمييز بين الدوائر مقابل الدوائر المتوازية. لدائرة سلسلة ، المقاومة الكلية (Rمجموع) هو مجرد مجموع المقاومة الفردية ، لذلك:
R_ {total} = R_1 + R_2 + R_3 + ...إن حقيقة كونها دائرة متسلسلة تعني أن المقاومة الكلية على المسار هي مجرد مجموع المقاومة الفردية على ذلك.
بالنسبة لمشكلة التدريب ، تخيل دائرة سلسلة بثلاث مقاومات: R1 = 2 Ω, R2 = 4 Ω و R3 = 6 Ω. حساب المقاومة الكلية في الدائرة.
هذا هو ببساطة مجموع المقاومة الفردية ، وبالتالي فإن الحل هو:
تبدأ {محاذاة} R_ {total} & = R_1 + R_2 + R_3 & = 2 ؛ أوميغا ؛ + 4 ؛ أوميغا ؛ +6 ؛ Omega & = 12 ؛ أوميغا نهاية {محاذاة}حساب المقاومة لدائرة موازية
للدوائر المتوازية ، وحساب Rمجموع هو أكثر تعقيدا قليلا. الصيغة هي:
{1 above {2pt} R_ {total}} = {1 above {2pt} R_1} + + {1 above {2pt} R_2} + {1 above {2pt} R_3}تذكر أن هذه الصيغة تمنحك المقاومة المتبادلة (بمعنى ، واحدة مقسومة على المقاومة). لذلك تحتاج إلى تقسيم واحد على الإجابة للحصول على المقاومة الكاملة.
تخيل أن هذه المقاومات الثلاثة نفسها من قبل تم ترتيبها بالتوازي بدلاً من ذلك. ستقدم المقاومة الكلية بواسطة:
start {align} {1 above {2pt} R_ {total}} & = {1 above {2pt} R_1} + + {1 above {2pt} R_2} + {1 above {2pt} R_3} & = {1 above {2pt} 2 ؛ Ω} + {1 above {2pt} 4 ؛ Ω} + {1 above {2pt} 6 ؛ Ω} & = {6 above {2pt} 12 ؛ Ω} + {3 above {2pt} 12 ؛ Ω} + {2 above {2pt} 12 ؛ Ω} & = {11 above {2pt} 12Ω} & = 0.917 ؛ {^ {- 1} end {محاذاة}لكن هذا هو 1 / Rمجموع، وبالتالي فإن الجواب هو:
تبدأ {محاذاة} R_ {total} & = {1 above {2pt} 0.917 ؛ {^ {- 1}} & = 1.09 ؛ أوميغا نهاية {محاذاة}كيفية حل سلسلة ودائرة الجمع الموازي
يمكنك تقسيم جميع الدوائر إلى مجموعات من السلاسل والدوائر المتوازية. قد يكون لفرع الدائرة المتوازية ثلاثة مكونات متتالية ، ويمكن أن تتألف الدائرة من سلسلة من ثلاثة أقسام متوازية ومتفرعة في صف واحد.
إن حل مثل هذه المشاكل يعني مجرد تقسيم الدائرة إلى أقسام والعمل عليها بدورها. خذ مثالاً بسيطًا ، حيث يوجد ثلاثة فروع على دارة متوازية ، لكن أحد هذه الفروع يحتوي على سلسلة من ثلاثة مقاومات متصلة.
إن حيلة حل المشكلة تتمثل في دمج حساب المقاومة المتسلسلة في الحساب الأكبر للدائرة بأكملها. لدائرة موازية ، يجب عليك استخدام التعبير:
{1 above {2pt} R_ {total}} = {1 above {2pt} R_1} + + {1 above {2pt} R_2} + {1 above {2pt} R_3}لكن أول فرع ، R1، مصنوع بالفعل من ثلاثة مقاومات مختلفة في السلسلة. لذلك إذا ركزت على هذا أولاً ، فأنت تعلم أن:
R_1 = R_4 + R_5 + R_6تخيل ذلك R4 = 12 Ω, R5 = 5 Ω و R6 = 3 Ω. المقاومة الكلية هي:
تبدأ {محاذاة} R_1 & = R_4 + R_5 + R_6 & = 12 ؛ أوميغا ؛ + 5 ؛ أوميغا ؛ + 3 ؛ Omega & = 20 ؛ أوميغا نهاية {محاذاة}مع هذه النتيجة للفرع الأول ، يمكنك الذهاب إلى المشكلة الرئيسية. مع المقاوم واحد على كل من المسارات المتبقية ، ويقول ذلك R2 = 40 Ω و R3 = 10 Ω. يمكنك الآن حساب:
start {align} {1 above {2pt} R_ {total}} & = {1 above {2pt} R_1} + + {1 above {2pt} R_2} + {1 above {2pt} R_3} & = {1 above {2pt} 20 ؛ Ω} + {1 above {2pt} 40 ؛ Ω} + {1 above {2pt} 10 ؛ Ω} & = {2 above {2pt} 40 ؛ Ω} + {1 above {2pt} 40 ؛ Ω} + {4 above {2pt} 40 ؛ Ω} & = {7 above {2pt} 40 ؛ Ω} & = 0.175 ؛ {^ {- 1} end {محاذاة}إذن هذا يعنى:
تبدأ {محاذاة} R_ {total} & = {1 above {2pt} 0.175 ؛ {^ {- 1}} & = 5.7 ؛ أوميغا نهاية {محاذاة}حسابات أخرى
من الأسهل حساب المقاومة على دارة متسلسلة مقارنة بالدائرة المتوازية ، لكن هذا ليس هو الحال دائمًا. معادلات السعة (C) في سلسلة والدوائر المتوازية تعمل أساسا في الاتجاه المعاكس حولها. بالنسبة لدائرة متسلسلة ، لديك معادلة لمعادلة السعة ، لذلك يمكنك حساب السعة الكلية (Cمجموع) مع:
{1 above {2pt} C_ {total}} = {1 above {2pt} C_1} + + {1 above {2pt} C_2} + {1 above {2pt} C_3} + ....ثم عليك تقسيم واحد على هذه النتيجة لتجد Cمجموع.
لدائرة موازية لديك معادلة أبسط:
C_ {total} = C_1 + C_2 + C_3 + ....ومع ذلك ، فإن النهج الأساسي لحل المشكلات المتعلقة بالسلسلة مقابل الدوائر المتوازية هو نفسه.