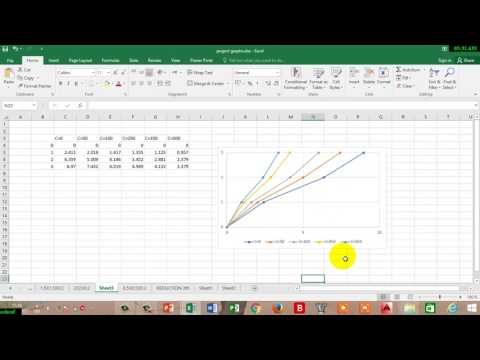
رسم بياني للمعادلات الخطية كخط مستقيم باستخدام شكل تقاطع الميل من y = mx + b ، حيث "m" هو الميل و "b" هو التقاطع y ، أو النقطة التي يعبر فيها الخط المحور y. يمكن استخدام تقاطع y للعثور على نقاط إضافية للخط. يمكن إضافة المنحدر ، الذي يمثل حركة على المحور ص تليها حركة على المحور س ، إلى التقاطع ص لإيجاد نقطة أخرى. على سبيل المثال ، منحدر 5 وتقاطع ص 3 ، أو نقطة (0،3) ، من شأنه أن يخلق نقطة إضافية من (0 + 1 ، 3 + 5) = (1،8).
رسم بياني لمعادلة خطية عن طريق تحويلها إلى شكل تقاطع الميل ، وتحديد الميل وتقاطع y ثم نقاط الرسم البياني ، بدءًا من التقاطع. استخدم المعادلة الخطية 6y = 6x + 5 كمثال. قسّم كلا الجانبين على 6: y = x + (5/6) ، حيث يكون الميل 1 وتقاطع y هو (5/6) أو نقطة (0،5 / 6).
تحويل التقاطع y الكسري إلى نموذج عشري لتسهيل الرسم البياني. اقسم البسط على المقام: 5/6 = 0.833 ... أو 0.83 (مدور). ارسم نقطة التقاطع y على الرسم البياني عن طريق تقدير بصري لنقطة على المحور ص التي تقل قليلاً عن 1.
ابحث عن نقاط إضافية للخط باستخدام الميل وتقاطع y في شكل عشري بإضافة المنحدر مرتين وطرح المنحدر مرتين ، لإعطاء رؤية أفضل لما يبدو عليه الخط. لاحظ أن الميل هو 1 أو 1/1: (0 + 1 ، 0.83 + 1) = (1،1.83) و (1 + 1 ، 1.83 + 1) = (2،2.83) ؛ (0 - 1 ، 0.83 - 1) = (-1 ، -0.17) و (-1 - 1 ، -0.17 - 1) = (-2 ، -1.17).
قم برسم النقاط ورسم خطًا مستقيمًا ، ووضع الأسهم على كل طرف لتمثيل استمرار.