
المحتوى
يشار إلى صور الدوال الرياضية كرسوم بيانية. يمكنك إنشاء رسومات بيانية ثنائية الأبعاد بمحور x و y أو رسومات ثلاثية الأبعاد ذات محور x و y و z. بافتراض رسم بياني ثنائي الأبعاد ، فإن معادلة الرياضيات سوف تعطي قيمة y كدالة x أو y = f (x). يشير ذلك إلى أنه مع تغير x ، ستتغير y وفقًا للدالة f (x). على سبيل المثال ، y = 2x هي وظيفة بسيطة حيث إذا كانت x = 2 و y = 4 وإذا كانت x = 6 و y = 12. يمكنك رسم هذه العلاقة بين x و y على رسم بياني لإنشاء تمثيل مرئي للعلاقة بين س و ص.
قم بإنشاء رسم بياني للمعادلة: y = 2x ،
- ••• Charley Steward / Demand Media
ارسم خطًا أفقيًا مستقيمًا على قطعة من الورق. تسمية السطر "س." قسّم الخط إلى 10 أقسام متساوية المسافات ، مع الإشارة إلى كل قسم بعلامات التجزئة الرأسية الصغيرة. تسمية علامات التجزئة من 1 إلى 10.

ارسم خطًا رأسيًا مستقيمًا ، بدءًا من النقطة التي بدأت فيها الخط الأفقي لـ x. تسمية هذا السطر "ص" قسِّم الخط إلى 20 قسمًا متساوية المسافات ، مع الإشارة إلى كل قسم بعلامات التجزئة الصغيرة الأفقية. تسمية علامات التجزئة من 1 إلى 20.
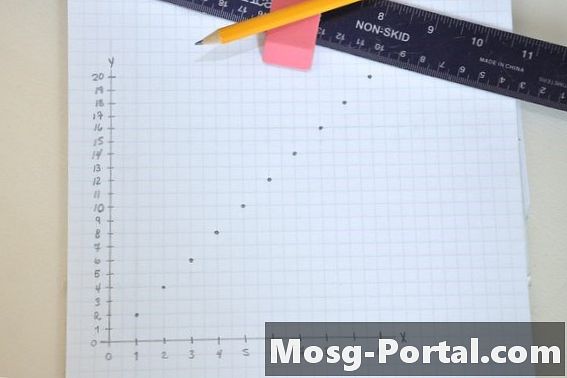
ارسم y = 2x. ابدأ بـ x = 1. في x = 1 ، y = 2. على الرسم البياني ، انتقل إلى علامة التجزئة على المحور السمي المسمى 1. بينما في 1 على المحور السيني ، صعد رأسياً إلى علامة التجزئة 2 على المحور ص ووضع "نقطة" في تلك المرحلة. الانتقال إلى x = 2. في x = 2 ، y = 4. على الرسم البياني ، انتقل إلى علامة التجزئة على المحور س المسمى 2. بينما في 2 على المحور س ، صعود عموديًا إلى علامة التجزئة 4 على المحور ص ووضع "نقطة" في تلك المرحلة. كرر هذه العملية طوال الطريق إلى x = 10.

ارسم خطًا يربط بين جميع النقاط. سيكون لديك خط مستقيم أشار إلى الأعلى. الخط المستقيم هو تمثيل رسومي أو مرئي للمعادلة y = 2x.
قم بإنشاء رسم بياني للمعادلة: y = sin (x) ،


ارسم خطًا مستقيمًا أفقيًا على قطعة من الورق. تسمية السطر "س." قسّم الخط إلى 10 أقسام متساوية المسافات ، مع الإشارة إلى كل قسم بعلامات التجزئة الرأسية الصغيرة. تسمية علامات التجزئة من 0 إلى 10.

ارسم خطًا رأسيًا مستقيمًا. ارسم الخط بحيث تكون بداية الخط الأفقي لـ x في منتصف الخط العمودي. بهذه الطريقة ، سيكون لديك نصف الخط العمودي أسفل الخط x - وهو الاتجاه السلبي - والنصف الآخر فوق الخط x - وهو الاتجاه الإيجابي. قسِّم الخط إلى 10 أقسام متساوية المسافات ، مع الإشارة إلى كل قسم بعلامات التجزئة الأفقية الصغيرة. سيكون لديك خمس علامات التجزئة في الاتجاه السلبي وخمس في الاتجاه الإيجابي. قم بتسمية علامات التجزئة في الاتجاه السلبي من 0 إلى -5 وعلامات التجزئة في الاتجاه الإيجابي من 0 إلى 5. ضع أيضًا أربع علامات تجزئة متساوية التباعد بين 0 و 1 في كل من الاتجاه الموجب والسالب. صنّفهم 0.2 و 0.4 و 0.6 و 0.8 في كلا الاتجاهين الإيجابي والسلبي.

ارسم الدالة y = sin (x). باستخدام حاسبة مع دالة الجيب ، ابدأ بـ x = 0. في x = 0 ، جيب 0 هو 0 ، لذلك y = 0. في الرسم البياني ، ضع نقطة في x = 0. في x = 1 ، الجيب من 1 هو 0.84 ، لذلك y = 0.84. انتقل إلى المحور س حيث x = 1 وتتبع ما يصل إلى المحور ص في ص = 0.84 ووضع نقطة في تلك المرحلة. كرر هذا لـ x = 2 إلى 10.
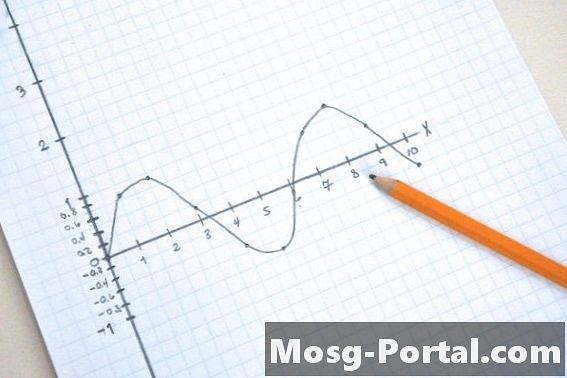
ارسم خطًا يربط بين جميع النقاط. سيكون لديك موجة جيبية تتأرجح ذهابًا وإيابًا بين المحور الإيجابي والسلبي. هذا هو التمثيل البياني أو المرئي للمعادلة y = sin (x).