
المحتوى
من أجل أن يكون الشكلان متطابقين ، يجب أن يكون لكل منهما نفس عدد الجوانب ويجب أن تكون زواياهما متماثلة أيضًا. تتمثل أسهل الطرق لتحديد ما إذا كان شكلان متطابقان في تدوير أحد الأشكال حتى يتم اصطفافه مع الآخر ، أو ببساطة تكديس الأشكال فوق بعضها البعض لمعرفة ما إذا كانت هناك أي أطراف تنتهي. إذا لم تتمكن من نقل الأشكال ماديًا ، يمكنك استخدام الصيغ لتحديد ما إذا كانت الأشكال متطابقة أم لا.
دوائر متطابقة
••• راي روبرت جرين / وسائل الإعلامجميع الدوائر لديها نفس زاوية 360 درجة. العامل الوحيد في تحديد مدى تطابق دائرتين هو مقارنة حجمها. القطر عبارة عن خط مستقيم من خلال مركز الدائرة من الحافة إلى الحافة ، في حين أن نصف قطر الدائرة هو الطول من مركزها إلى الحافة الخارجية. سيثبت قياس أيٍّ من هاتين الدورتين في كلتا الدائرتين إذا كانا متطابقين.
متوازيات الأضلاع
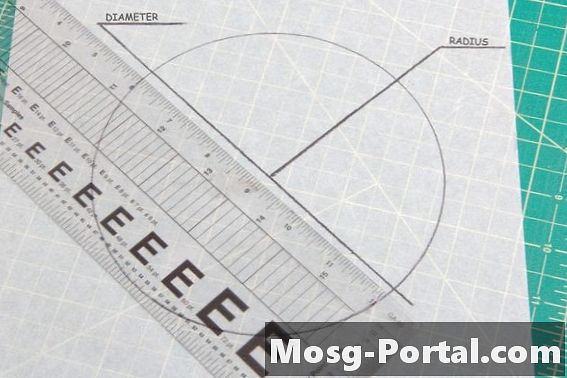
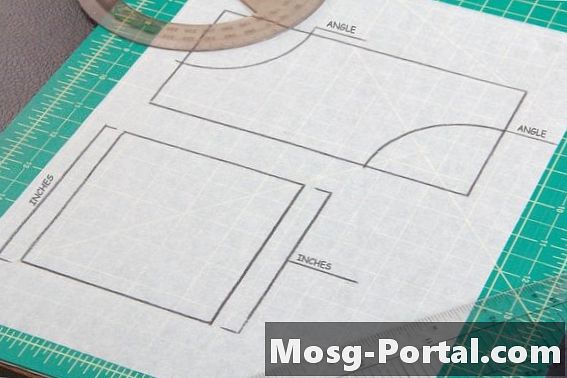
يحتوي المخطط المتوازي على اثنين من أزواج الجانبين المتوازيين ، مثل المربعات والمستطيلات. يكون للجانبين أو زوايا متوازي الأضلاع نفس القياس ، لذلك من الضروري أخذ قياسين زاوية أو جانبيين في متوازي الأضلاع ، أحدهما من كل زوج من الأضلاع ، من أجل مقارنة التطابق مع شكل آخر.
مثلثات
••• راي روبرت جرين / وسائل الإعلاممن أجل العثور على تطابق المثلثات ، تحتاج إلى تحديد حجم كل زاوية أو جانب ، لأن الثلاثة يمكن أن تكون مختلفة. هناك ثلاثة افتراضات يمكن استخدامها لتحديد مثلثات متطابقة. افتراض SSS هو عندما تقيس الجوانب الثلاثة لكل مثلث. توضح افتراضات ASA ما إذا كانت أي زاويتين وجانب الاتصال الخاص بهما يتطابقان مع المثلث الآخر ، فهما متطابقان. تقوم افتراضات SAS بالعكس ، حيث تقيس الجانبين وزاوية الاتصال الخاصة بهم للمقارنة مع المثلث الآخر.
نظريات المثلثات المتطابقة

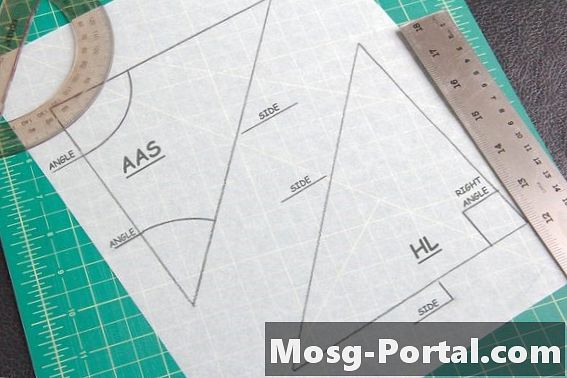
هناك نظريتان مفيدتان لإيجاد مثلثات متطابقة. تقول نظرية AAS أنه إذا كانت زاويتان وجانب لا يربط بينهما مساويا لمثلث آخر ، فإنهما متطابقان. تنطبق نظرية Hypotenuse-Leg فقط على المثلثات بزاوية 90 درجة أو "يمين". هذا عندما تقيس الوتر - الجانب المقابل لزاوية 90 درجة - وواحد من الجوانب الأخرى للمثلث ، للمقارنة مع الشكل الآخر.