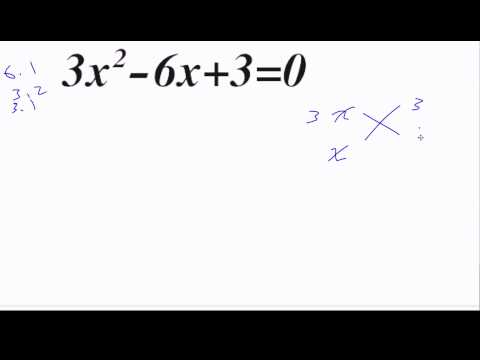
المحتوى
تستخدم المعادلات التربيعية فعليًا في الحياة اليومية ، كما هو الحال عند حساب المناطق ، وتحديد ربح المنتجات أو صياغة سرعة كائن ما. تشير المعادلات التربيعية إلى معادلات بها متغير مربع واحد على الأقل ، مع أن النموذج الأكثر نموذجية هو ax² + bx + c = 0. تمثل الحرف X غير معروف ، و ab و c هي المعاملات التي تمثل الأرقام المعروفة والحرف a غير متساوية إلى الصفر.
حساب مناطق الغرفة
يحتاج الناس في كثير من الأحيان إلى حساب مساحة الغرف أو الصناديق أو قطع الأرض. مثال قد يتضمن بناء مربع مستطيل حيث يجب أن يكون جانب واحد ضعف طول الجانب الآخر. على سبيل المثال ، إذا كان لديك 4 أقدام مربعة فقط من الخشب لاستخدامها في الجزء السفلي من المربع ، مع هذه المعلومات ، يمكنك إنشاء معادلة لمنطقة المربع باستخدام نسبة الجانبين. هذا يعني أن المساحة - طول أوقات العرض - من حيث x تساوي x مرات 2x ، أو 2x ^ 2. يجب أن تكون هذه المعادلة أقل من أو تساوي أربعة لإنشاء مربع بنجاح باستخدام هذه القيود.
معرفة الربح
في بعض الأحيان يتطلب حساب ربح تجاري استخدام دالة تربيعية. إذا كنت ترغب في بيع شيء ما - حتى شيء بسيط مثل عصير الليمون - فأنت بحاجة إلى تحديد عدد العناصر التي تنتجها حتى تحقق ربحًا. دعنا نقول ، على سبيل المثال ، أنك تبيع أكواب من عصير الليمون ، وتريد صنع 12 كوبًا. أنت تعلم ، مع ذلك ، أنك ستبيع عددًا مختلفًا من النظارات وفقًا للطريقة التي تحدد بها سعرك. بسعر 100 دولار للزجاج ، من غير المحتمل أن تبيع أيًا منها ، ولكن بسعر 0.01 دولار للزجاج ، من المحتمل أن تبيع 12 كوبًا في أقل من دقيقة. لذلك ، لتحديد مكان تعيين السعر الخاص بك ، استخدم P كمتغير. لقد قدرت أن الطلب على أكواب عصير الليمون يكون عند 12 - P. وبالتالي ، سيكون عائدك هو سعر ضرب عدد النظارات المباعة: P مرة 12 ناقص P ، أو 12P - P ^ 2. باستخدام مقدار تكاليف إنتاج عصير الليمون ، يمكنك ضبط هذه المعادلة على هذا المبلغ واختيار سعر من هناك.
التربيعية في ألعاب القوى
في الأحداث الرياضية التي تنطوي على إلقاء أشياء مثل وضع اللقطة أو الكرات أو الرمح ، تصبح المعادلات التربيعية مفيدة للغاية. على سبيل المثال ، يمكنك رمي كرة في الهواء وجعل صديقك يمسك بها ، لكنك تريد أن تمنحها الوقت المحدد للوصول إلى الكرة. استخدم معادلة السرعة ، والتي تحسب ارتفاع الكرة بناءً على معادلة مكافئ أو تربيعي. ابدأ برمي الكرة على ارتفاع 3 أمتار ، حيث توجد يديك. افترض أيضًا أنه يمكنك رمي الكرة لأعلى بسرعة 14 مترًا في الثانية ، وأن جاذبية الأرض تقلل من سرعة الكرات بمعدل 5 أمتار في الثانية. من هذا ، يمكننا حساب الارتفاع ، h ، باستخدام المتغير t للوقت ، في شكل h = 3 + 14t - 5t ^ 2. إذا كانت أيدي أصدقائك على ارتفاع 3 أمتار ، فكم ثانية ستستغرق الكرة للوصول إليها؟ للإجابة على هذا ، قم بتعيين المعادلة تساوي 3 = h ، وحل لـ t. الجواب حوالي 2.8 ثانية.
العثور على السرعة
المعادلات التربيعية مفيدة أيضًا في حساب السرعات. على سبيل المثال ، يستخدم كاياكرز متعطشين للمعادلات التربيعية لتقدير سرعتهم عند الصعود والنزول في النهر. لنفترض أن أحد قوارب الكاياك يصعد في النهر ، وأن النهر يتحرك بسرعة كيلومترين في الساعة. إذا ذهب في اتجاه التيار المعاكس على ارتفاع 15 كم ، واستغرقته الرحلة 3 ساعات للذهاب إلى هناك والعودة ، تذكر أن الوقت = المسافة مقسومة على السرعة ، واسمحوا v = سرعة الزوارق بالنسبة إلى الأرض ، ودع x = سرعة الزوارق في الماء. أثناء السفر لأعلى ، تكون سرعة الزوارق هي v = x - 2 - طرح 2 للمقاومة من تيار النهر - وأثناء السير في اتجاه المصب ، تكون سرعة قوارب الكاياك v = x + 2. إجمالي الوقت يساوي 3 ساعات ، وهو ما يساوي الوقت الذي يتم فيه الوصول إلى المنبع بالإضافة إلى الوقت الذي يتم الوصول إليه في اتجاه مجرى النهر ، وتبعد كلا المسافة 15 كم. باستخدام معادلاتنا ، نعلم أن 3 ساعات = 15 / (س - 2) + 15 / (س + 2). بمجرد أن يتم توسيع هذا جبريًا ، نحصل على 3x ^ 2 - 30x -12 = 0. حل لـ x ، نعلم أن kayaker قد حرك قوارب الكاياك بسرعة 10.39 كم في الساعة.