كيفية العثور على نسبة مشتركة من الكسر

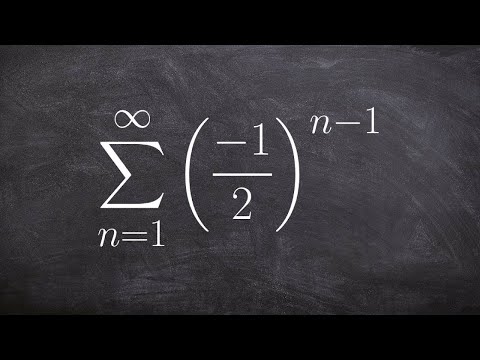
إن حساب النسبة الشائعة لسلسلة هندسية هي مهارة تتعلمها في حساب التفاضل والتكامل وتستخدم في مجالات تتراوح من الفيزياء إلى الاقتصاد. تحتوي السلسلة الهندسية على النموذج "a * r ^ k" ، حيث "a" هو المصطلح الأول من السلسلة ، "r" هي النسبة الشائعة و "k" هي متغير. شروط السلسلة في كثير من الأحيان الكسور. النسبة الشائعة هي الثابت الذي تضربه كل فصل لتوليد المصطلح التالي. يمكنك استخدام النسبة الشائعة لحساب مجموع السلسلة.

اكتب أي مصطلحين متسلسلين من السلسلة الهندسية ، ويفضل أن يكون الأولان. على سبيل المثال ، إذا كانت سلسلتك 3/2 + -3/4 + 3/8 + -3/16 + .. يمكنك استخدام 3/2 و -3/4.

قسّم الفصل الثاني على الفصل الأول لإيجاد النسبة المشتركة. لتقسيم الكسور ، اقلب المقسوم واجعله الضرب. باستخدام المثال السابق مع 3/2 و -3/4 ، تكون النسبة الشائعة (-3/4) / (3/2) = (-3/4) * (2/3) = -6/12 = - 1/2.

استخدم النسبة الشائعة ، المصطلح الأول والعدد الإجمالي للمصطلحات لحساب مجموع السلسلة. إذا كان لديك عدد محدد من المصطلحات ، فاستخدم الصيغة "a * (1-r ^ n) / (1-r)" ، حيث "a" هي المصطلح الأول ، و "r" هي النسبة الشائعة و "n" هو عدد المصطلحات. استخدم الصيغة "a / (1-r)" إذا كانت السلسلة لانهائية ، حيث "a" هو المصطلح الأول و "r" هي النسبة الشائعة. يجب أن تقترب المصطلحات من 0 حتى تتقارب السلسلة وتحصل على مبلغ. باستخدام المثال السابق ، فإن النسبة الشائعة هي -1/2 ، والمصطلح الأول هو 3/2 والسلسلة غير محدودة ، وبالتالي فإن المجموع هو "(3/2) / (1 - (- 1/2)) = 1 ".