
المحتوى
يمكن للدوائر الكهربائية ترتيب عناصر دوائرها في سلسلة أو متوازية. في دوائر السلسلة ، يتم توصيل العناصر باستخدام نفس الفرع الذي التيار الكهربائي من خلال كل واحد منهم واحد تلو الآخر. في الدوائر المتوازية ، للعناصر فروعها الخاصة المنفصلة. في هذه الدوائر ، يمكن أن يأخذ التيار مسارات مختلفة طوال الوقت.
لأن التيار يمكن أن يأخذ مسارات مختلفة في دارة متوازية ، فإن التيار ليس ثابتًا عبر دارة متوازية. بدلاً من ذلك ، بالنسبة للفروع المتصلة بالتوازي مع بعضها البعض ، فإن الجهد أو الانخفاض المحتمل عبر كل فرع ثابت. وذلك لأن التيار يوزع نفسه عبر كل فرع بكميات تتناسب عكسيا مع مقاومة كل فرع. هذا يسبب أن يكون التيار هو أكبر مكان تكون فيه المقاومة أقل والعكس صحيح.
تتيح هذه الصفات للدوائر المتوازية السماح بتدفق الشحنة عبر مسارين أو أكثر ، مما يجعلها مرشحًا قياسيًا في المنازل والأجهزة الكهربائية من خلال نظام طاقة مستقر وفعال. إنها تتيح تدفق الكهرباء عبر أجزاء أخرى من الدائرة عند تلف جزء أو كسره ، ويمكنه توزيع الطاقة بالتساوي عبر المباني المختلفة. يمكن إظهار هذه الخصائص من خلال رسم تخطيطي ومثال للدائرة الموازية.
مخطط الدائرة الموازية
نصائح
أمثلة الدوائر المتوازية
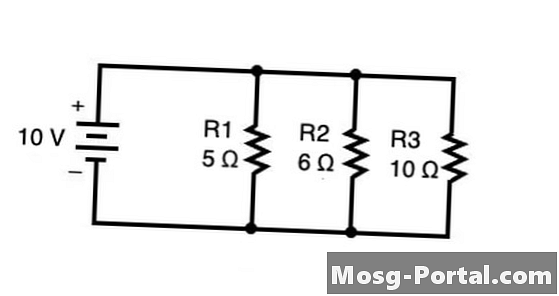
لإيجاد المقاومة الكاملة للمقاومات مرتبة بالتوازي مع بعضها البعض ، استخدم الصيغة 1 / Rمجموع = 1 / R1 + 1 / R2 + 1 / R3 + ... + 1 / Rn حيث يتم تلخيص مقاومة كل المقاوم على الجانب الأيمن من المعادلة. في الرسم البياني أعلاه ، يمكن حساب المقاومة الكلية بالأوم (Ω) على النحو التالي:
لاحظ أنه لا يمكنك سوى "قلب" طرفي المعادلة من الخطوة 3 إلى الخطوة 4 عندما يكون هناك مصطلح واحد فقط على طرفي المعادلة (في هذه الحالة ، 1 / Rمجموع على اليسار و 14/30 Ω على اليمين).
بعد حساب المقاومة ، يمكن حساب التيار والجهد باستخدام قانون أوم V = I / R بحيث الخامس هو قياس الجهد في فولت ، أنا يقاس الحالية في الامبير ، و R هي المقاومة في أوم. في الدوائر المتوازية ، يكون مجموع التيارات عبر كل مسار هو إجمالي التيار من المصدر. يمكن حساب التيار في كل المقاوم في الدائرة عن طريق ضرب المقاومة مرات الجهد للمقاوم. يظل الجهد ثابتًا في جميع أنحاء الدائرة ، لذا فإن الجهد هو مصدر الجهد للبطارية أو الجهد.
دائرة موازية مقابل سلسلة
••• سيد حسين آذرفي الدوائر المتسلسلة ، يكون التيار ثابتًا طوال الوقت ، ويعتمد انخفاض الجهد على مقاومة كل المقاوم والمقاومة الكلية هي مجموع كل المقاوم على حدة. في الدوائر المتوازية ، يكون الجهد ثابتًا طوال الوقت ، ويعتمد التيار على كل المقاوم وعكس المقاومة الكلية هو مجموع معكوس كل المقاوم على حدة.
يمكن استخدام المكثفات والمحاثات لتغيير الشحنة في السلسلة والدوائر المتوازية مع مرور الوقت. في سلسلة الدوائر ، المجموع السعة من الدائرة (التي قدمها المتغير C) ، وإمكانات مكثف لتخزين تهمة مع مرور الوقت ، هو مجموع معكوس من ينعكس كل السعة الفردية ، و الحث الكلي (أنا) ، قوة المحاثات لإعطاء قبالة تهمة مع مرور الوقت ، هو مجموع كل مغو. على النقيض من ذلك ، في الدائرة الموازية ، تكون السعة الكلية هي مجموع كل مكثف فردي ، وعكس الحث الكلي هو مجموع الانعكاسات لكل محاثة فردية.
سلسلة والدوائر المتوازية لها أيضا وظائف مختلفة. في سلسلة دائرية ، إذا تم كسر جزء واحد ، فلن يتدفق التيار عبر الدائرة على الإطلاق. في دائرة موازية ، يتوقف فتح الفرع الفردي فقط عن التيار في هذا الفرع. ستستمر بقية الفروع في العمل لأن التيار يحتوي على مسارات متعددة يمكن أن يأخذها عبر الدائرة.
سلسلة موازية الدائرة

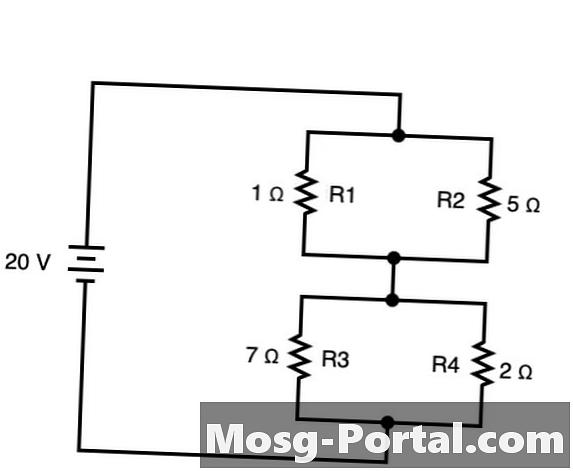
الدوائر التي تحتوي على كل من العناصر المتفرعة المرتبطة أيضًا بحيث يتدفق التيار في اتجاه واحد بين هذين الفرعين على حد سواء سلسلة وبالتوازي. في هذه الحالات ، يمكنك تطبيق القواعد من كل من السلسلة والتوازي حسب الاقتضاء للدائرة. في المثال أعلاه ، R1 و R2 هي بالتوازي مع بعضها البعض لتشكيل R5و كذلك R3 و R4 لتشكيل R6. يمكن تلخيصها بالتوازي على النحو التالي:
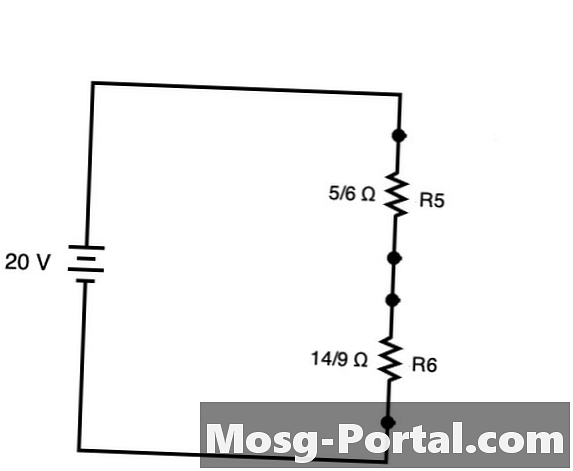
يمكن تبسيط الدائرة لإنشاء الدائرة الموضحة أعلاه مباشرة مع R5 و R6. يمكن إضافة هذين المقاومات مباشرة كما لو كانت الدائرة سلسلة.
Rمجموع = 5/6 Ω + 14/9 Ω = 45/54 Ω + 84/54 Ω = 129/54 Ω = 43/18 Ω أو حوالي 2.38 Ω
مع 20 الخامس كما الجهد ، يملي قانون أوم أن إجمالي الحالي يساوي V / Rأو 20V / (43/18 Ω) = 360/43 A أو عن 8.37 مع هذا التيار الكلي ، يمكنك تحديد انخفاض الجهد عبر كل من R5 و R6 باستخدام قانون أوم (V = I / R) كذلك.
إلى عن على R5, V5 = 360/43 A x 5/6 Ω = 1800/258 V أو عن 6.98 V.
إلى عن على R6, V6 = 360/43 A x 14/9 Ω = 1680/129 V أو عن 13.02
وأخيرا ، هذه الجهد يسقط ل R5 و R6 يمكن تقسيمها مرة أخرى إلى الدوائر المتوازية الأصلية لحساب الحالي من R1 و R2 إلى عن على R5 و R2 و R3 إلى عن على R6 باستخدام قانون أوم.
I1 = (1800/258 V) / 1 Ω = 1800/258 A أو abou_t 6.98 A._
I2 = (1800/258 فولت) / 5 Ω = 1500/43 أ أو abou_t 34.88 A._
I3 = (680/129 V) / 7 Ω = 4760/129 أ أو عن 36.90 أ.
I3 = (680/129 V) / 2 Ω = 1360/129 أ أو عن 10.54